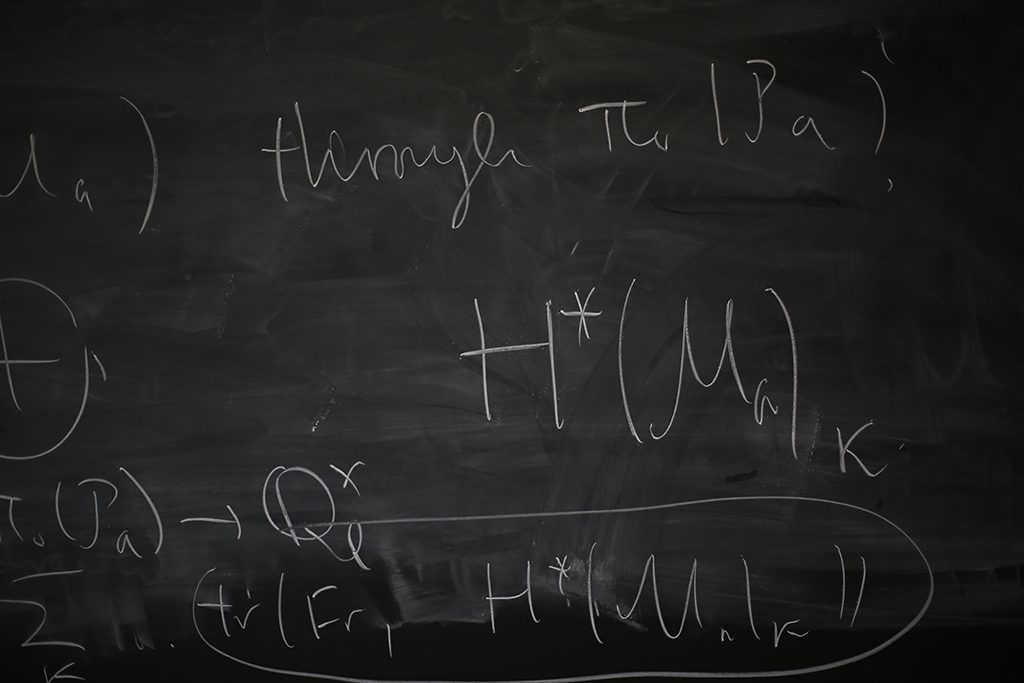Faithfully Flat [Phẳng Chung Thủy]

Installation Ongoing Project Performance Art

Medium: multi media installation project based on a series of the durational performance art pieces as the essential original material for the installation / dự án sắp đặt đa phương tiện, sử dụng các chuỗi trình diễn kéo dài làm chất liệu cốt lõi cho tác phẩm sắp đặt

Venue:
PHASE 1 (started 2014)
+ 1:30 of scale installation & artist’ books showcase. VIASM – Institute for Advanced Study in Mathematics & Manzi Art Space – Hanoi, Vietnam – Jul 2014 view detail

+ North Branch Projects. Chicago. USA – Jun 2014 view detail

+ Joan Flasch Artists’ Book Collection. School of the Art Institute of Chicago. USA – May 2014 view detail

PHASE 2 (started 2020)
+ MoT+++. Ho Chi Minh City, Vietnam. Group exhibition: password 0~1 – June 2020 view detail

Faithfully in Latin is fideliter
Flat in Latin is planus

In mathematical language, faithfully flat means flat plus surjective. A faithfully flat module is always flat and faithful. But generally the converse does not hold.

In our conversation, I asked Ngo Bao Chau, who is best known for proving the fundamental lemma for automorphic form proposed by Robert Langlands and Diana Shelstad, how to visualize the term faithfully flat in terms of language in general, Dr. Ngo responded: “While a screw is a threaded fastener used to hold objects together, faithfully flat can be visualized as a screw to hold the origin of modified mathematical patterns.”

I apply the term faithfully flat used in mathematic for the title of my ongoing art project. This project, which is seemingly paradoxical to the meaning of the title, has arisen from my long-held fascination for the form of the dislocation of language and the conceptual space opened up within interpretation. I am also concerned about the connection between language and its own visual form, in terms of structure or sound. I imagine those dislocations, gaps and the shifts have been shaped in a world where languages are interpreted in different ways, structurally, systematically and vocally, where people lose each other and lose themselves, where all torn pieces of different cultures, histories and human knowledge are collaged together. Here, faithfully flat can be understood as ‘the virtual place’ that contains the crucial code to decipher any kind of languages. It holds the identity, the truth, and the origin. Does that place really exist? To explore the answer, I started my journey since the beginning of 2013, thinking – reading – performing – building this phase-to-phase project.

Here, all words written on the black board appeared and are absorbed by the artist, who has a little access to the advanced mathematical language, as images and as concepts. Following and imitating every white chalk line on the black board made by the mathematician, I put the ‘focal stress’ not on the time-based act of performing itself, but on the product or the aftermath created by the time-based performances which was to trace an unknown language through the performance artist.

Dr. Ngo was invited to interact in Phase One by layering the transparent papers onto the sketches, page by page, where mathematical language was converted into visual language with a lot of gaps in terms of misinterpretation and then he would try to fill the gaps. In his effort to correct the sketches, he was also lost at times to understand what was written down by the performer, and as a result, he would mark a smiley face or a question mark onto the obscure image. To the artist, the mathematician has been creating a concrete poetry with abstract spirit. The empty spaces formed around his words and symbols in the transparent papers can be seen as faithfully flat.

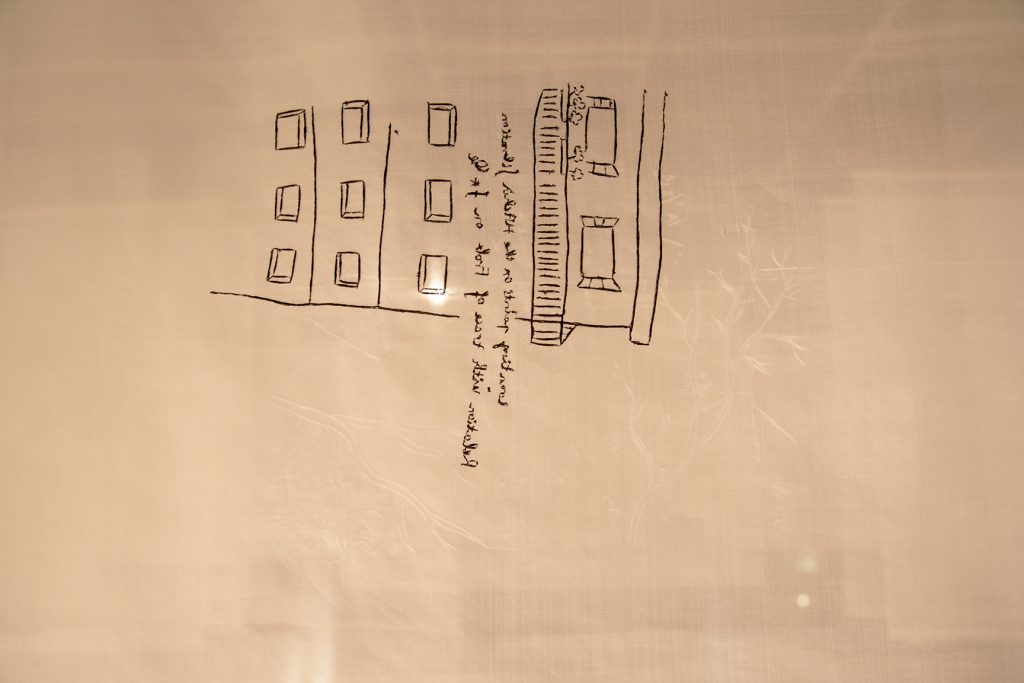
The products of these two no-audience-durational-performances – the sketches drawn by the artist and the corrections made by the mathematician, was sent to embroiderers to trace and embroider the lines in silver and black, respectively, onto thin silk. In this third process, the visual images and its languages have been shifted and modified one more time.

Andy Warhol said: “I am afraid that if you look at a thing long enough, it loses all of its meaning.” I understand this phrase in the context that when we look at a thing long enough, it loses all of its original meaning to open a totally new meaning for the same physical thing. That is what I experienced when I performed in the advanced mathematics class.

I invite the audience step into the faithfully flat world. The installation also includes sound installation – the sounds from the classroom of Dr. Ngo Bao Chau where I performed from January 1st to March 13th, 2014 were recorded then mixed to create the sound of a faithfully flat world.

This project won’t be possible without the collaboration of Dr. Ngo Bao Chau, the sponsor of Joan Flasch Artists’ Books Collection, and the Fulbright Program.

*

Faithfully theo tiếng Latin là fideliter (một cách trung thành). Flat theo tiếng Latin là planus (phẳng).

Thuật ngữ Faithfully Flat, Phẳng Chung Thủy, hay được nhắc đến trong bài giảng Affine Grassmannian của giáo sư Ngô Bảo Châu, người nổi tiếng với công trình chứng minh bổ đề cơ bản về dạng thức tự đẳng cấu do Robert Langlands và Diana Shelstad đề xuất. Thí dụ:

Bổ đề 4.1.
Cho E là một G-torsor trên Spec (R[[t]]). Tồn tại một R-đại số phẳng chung thuỷ R’ sao cho G-torsor cảm sinh trên Spec (R’[[t]]) là tầm thường. Hơn nữa, tồn tại một dãy khớp groupoid
<photo>

Trong cuộc hội thoại với giáo sư Ngô Bảo Châu, tôi hỏi ông có cách nào thị giác hoá thuật ngữ phẳng chung thủy theo như ngôn ngữ thông thường. Giáo sư Châu đáp: “Nếu một cái đinh ốc là một cái chốt có ren để gắn giữ các vật vào nhau, thì phẳng chung thủy có thể được hình dung như một cái đinh ốc gắn giữ nguồn gốc của những dạng toán đã được biến đổi!

Tôi mượn thuật ngữ toán học phẳng chung thủy làm tựa đề cho dự án nghệ thuật đang triển khai của mình. Dự án này, có vẻ như nghịch lý với nghĩa của tựa đề, đã khởi lên từ nỗi ám ảnh kéo dài của tôi về hình dạng của các biến lệch trong ngôn ngữ và cái không gian ý niệm được khơi mở trong vòng những diễn dịch khác nhau. Tôi cũng quan tâm tới mối quan hệ giữa ngôn ngữ với hình thức thị giác của chính nó, về mặt cấu trúc và âm thanh. Tôi hình dung những biến lệch, khoảng hổng và dịch chuyển này của ngôn ngữ được thành hình trong một thế giới nơi các ngôn ngữ được diễn dịch theo những cách khác nhau, theo cấu trúc, theo hệ thống và theo âm giọng, nơi mọi người lạc mất nhau và lạc mất bản thân mình, nơi mọi mảnh xé rời của những nền văn hoá, lịch sử khác nhau và tri thức của nhân loại được dán ghép. Vậy, phẳng chung thủy có thể được hiểu như địa điểm ảo chứa đựng bộ mã then chốt giải mã mọi kiểu ngôn ngữ – nắm giữ căn tính, sự thật, và gốc gác của mọi sự.

Triển lãm sắp đặt này là kết quả của Giai đoạn Một của dự án Phẳng Chung Thủy, với tỷ lệ 1:30.

Giai đoạn Một có thể được xem như một phòng thí nghiệm, được thành hình bằng một loạt trình diễn không khán giả của tôi, ngoại trừ 15 sinh viên khoa Toán ngồi cùng một phòng với tôi, và họ không hề biết tôi đang trình diễn. Những loạt trình diễn không khán giả này diễn ra 2 ngày mỗi tuần, kéo dài 1 giờ 50 phút mỗi ngày, tại lớp học Affine Grassmannian của Ngô Bảo Châu, giáo sư Toán của Đại học Chicago, từ ngày 9 tháng Giêng đến 13 tháng Ba năm 2014. Xem toán học cao cấp là một ngôn ngữ rất hạn chế sự tiếp nhận của người thường, trong trình diễn này tôi trở thành một “người ký hoạ” không hiểu gì, chỉ đơn giản chép lên sổ vẽ tất cả ngôn ngữ toán và các hình ảnh mà giáo sư Châu viết trên bảng đen để giải thích, chứng minh Bổ đề cơ bản của ông cho sinh viên. Ở đây, nghệ sĩ, vốn không hiểu gì về ngôn ngữ toán cao cấp, đã hấp thụ mọi từ ngữ ghi trên bảng đen như những hình ảnh và ý niệm. Lần theo và bắt chước từng đường phấn trên bảng đen do nhà toán học tạo nên, tôi đặt điểm nhấn không phải vào hành động trình diễn dùng thời gian làm căn tính, mà vào sản phẩm hoặc hậu quả được tạo ra bởi các buổi trình diễn dùng thời gian làm căn tính đó, khi lần theo một ngôn ngữ xa lạ với mình.

Giáo sư Châu được mời tương tác trong Giai đoạn Một bằng việc đặt từng trang giấy can lên các bản vẽ của tôi – nơi ngôn ngữ toán đã được chuyển đổi thành ngôn ngữ thị giác. Ông tìm cách lấp đầy những khoảng hồng được tạo ra bởi sự diễn dịch sai. Trong nỗ lực chỉnh lại các bức ký hoạ, nhiều lúc ông cũng hoang mang, không hiểu người trình diễn vẽ viết gì, và kết quả là, ông vẽ một mặt cười hay dấu hỏi chồng lên hình ảnh khó hiểu. Với nghệ sĩ, nhà toán học đã sáng tạo nên một hình thức thơ cụ thể với tinh thần trừu tượng.

Sản phẩm của hai cuộc durational performance không có khán giả ấy – những phác hoạ mà nghệ sĩ vẽ và những sửa chữa của nhà toán học – được gửi cho thợ thêu. Họ lần theo các đường nét và thêu lần lượt bằng chỉ bạc và đen, lên lụa mỏng. Ở quá trình thứ ba này, các hình ảnh thị giác và ngôn ngữ của nó lại một lần nữa bị biến đổi.

Dự án này được thực hiện với sự cộng tác của Giáo sư Ngô Bảo Châu.